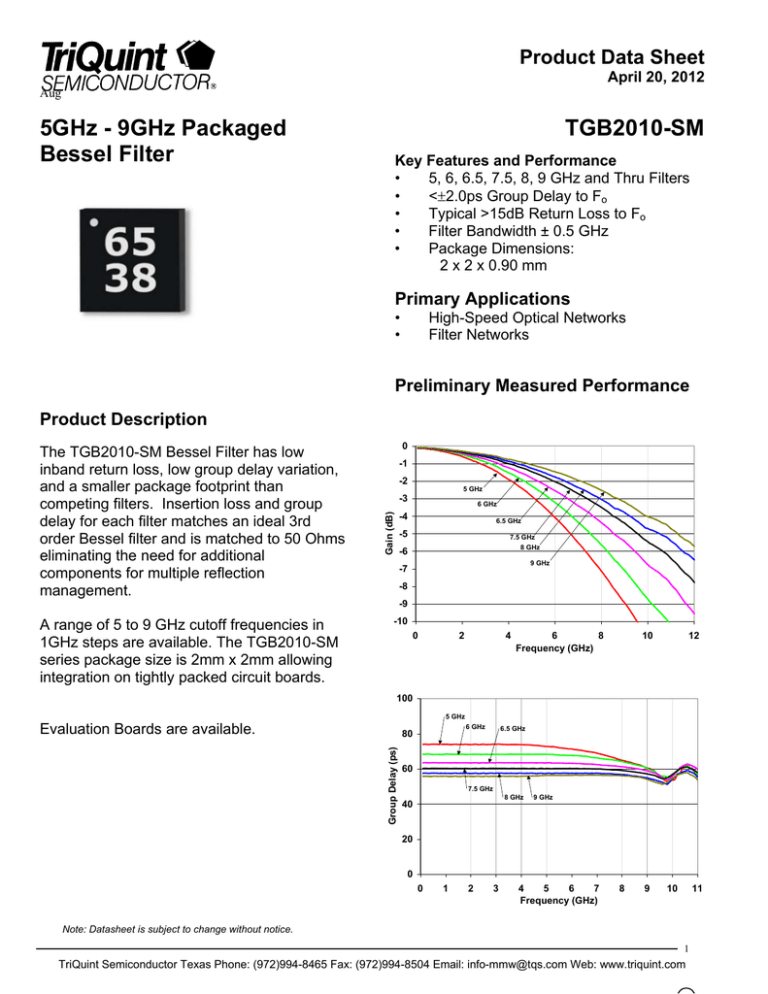
Bessel-Filter

Ein Bessel-Filter (auch als Bessel-Thomson-Filter bezeichnet) ist ein Frequenzfilter, bei dessen Entwurf folgende (äquivalente) Eigenschaften angestrebt werden:

optimales „Rechteckübertragungsverhalten“, d. h. eine Wellenform, deren Frequenzanteile innerhalb des Durchlassbereichs des Filters liegen, erscheint (bis auf eine Verzögerung) nahezu unverändert am Ausgang;
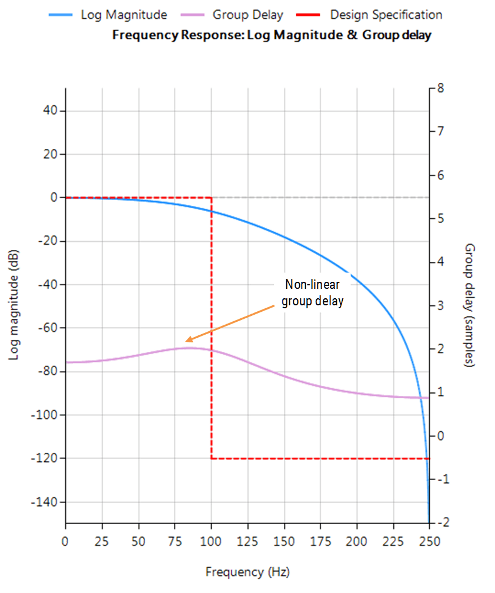
konstante Gruppenlaufzeit im Durchlassbereich;
linearer Phasengang im Durchlassbereich.

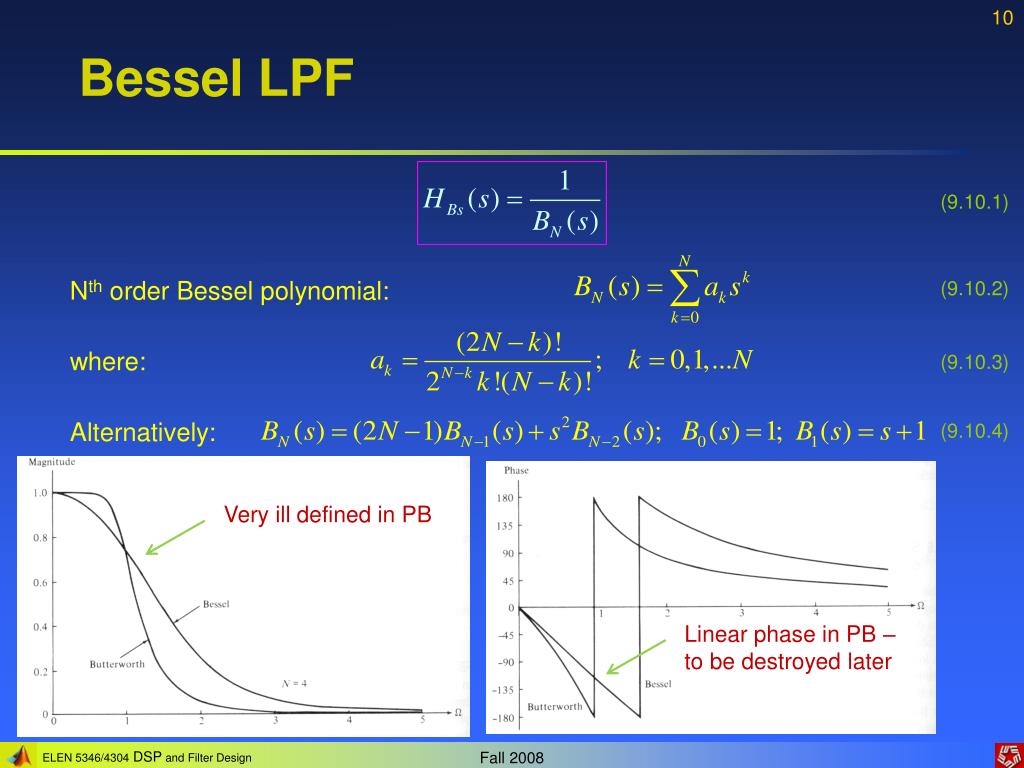
Dabei wird in Kauf genommen, dass der Amplitudenverlauf nicht so scharf wie beim Butterworth-Filter oder Tschebyscheff-Filter abknickt.

Das Filter wurde 1949 von W.E. Thomson als – hinsichtlich der Gruppenlaufzeit – optimales passives Verzögerungsnetzwerk entwickelt und nach dem deutschen Mathematiker Friedrich Wilhelm Bessel (1784–1846) benannt.

In der digitalen Signalverarbeitung können Bessel-Filter durch Wahl entsprechender Filterkoeffizienten in IIR-Filtern (rekursive Filterstruktur) realisiert werden.

Übertragungsfunktion

Die Übertragungsfunktion ist darauf optimiert, die Gruppenlaufzeit von der Frequenz unabhängig zu machen.

Mit der Übertragungsfunktion für ein Filter n-ter Ordnung

{\underline {A}}={\frac {A_{0}}{1 \sum _{i=1}^{n}c_{i}^{\prime }P^{i}}}

mit

A_{0}

Gleichspannungsverstärkung

P={\frac {p}{\omega _{g}}}\Leftrightarrow j\Omega =j{\frac {\omega }{\omega _{g}}}

und

\omega _{g}

Grenzfrequenz

lässt sich für die Koeffizienten $c_{i}^{\prime }$ die Rekursionsformel

ermitteln.

Die Koeffizienten sind allerdings nicht auf die Grenzfrequenz normiert, sondern auf die Gruppenlaufzeit, d. h. bei $\Omega =1$ ist die Amplitude nicht um 3 dB abgesunken. In finden sich diese Koeffizienten auf die Grenzfrequenz umgerechnet sowie die Koeffizienten aller Einzelfilter bis zur zehnten Ordnung.

Eigenschaften

Das Bessel-Filter besitzt folgende Eigenschaften:

glatter Frequenzverlauf im Durchlassbereich
geringe Steilheit des Amplitudengangs (geringer als beim Butterworth-Filter) im Bereich der Grenzfrequenz
geringes Überschwingen bei der Sprungantwort, verringert sich mit der Ordnung
konstante Gruppenlaufzeit im Durchlassbereich